Bryan Kelly, Seth Pruitt, Yinan Su. "Characteristics are Covariances: A Unified Model of Risk and Return." Journal of Financial Economics 2019
A new modeling approach for the cross section of average returns is proposed, called Instrumented Principal Components Analysis (IPCA). IPCA estimates market risk factors and loadings by allowing factor loadings to partially depend on observable asset characteristics. These observable characteristics act as instrumental variables for the latent conditional factor loadings. As a result, IPCA allows factor models to account for the fact that stock characteristics provide reliable conditioning information for average returns. IPCA also allows for modeling without the presumption that the researcher can specify factors beforehand and incorporates time-varying instruments that make it possible to estimate dynamic factor loadings. This allows for analysis of time-varying characteristics of stocks that lead to a better understanding of how stocks evolve over time.
Results and Findings
Results of the IPCA are markedly improved from previous results in asset pricing. Using a specification of four factors and restricting stock-level intercepts to zero, IPCA achieves a total R2 for returns of 19.4%. Comparatively, the Fama-French Five Factor model sample total R2 for returns is 21.9%. In the four factor IPCA model, the estimated compensation for factor exposures shows a predictive R2 for returns of 1.8%. In the matched sample, the predictive R2 for returns of the Fama-French five factor model is 0.3%. Out of sample predictive R2 for returns of the four-factor IPCA is 0.7%, which is still notably improved from the in-sample R2 of the Fama-French five factor model.
To achieve these results, the IPCA reduces the dimensionality of the parameter space by linking factor loadings to observable data. It does this by redefining the identity of a stock by its characteristics and not by a unique identifier. Once the characteristics are known, only a small number of parameters are needed to map the observed characteristics to betas.
The IPCA's ability to explain differences in average returns is a result of the restriction of intercept coefficients to zero for all stocks, effectively allowing intercepts to depend on stock characteristics. This can be considered a test of whether characteristics explain expected returns.
Including alphas in the one-factor IPCA model improves the model's ability to explain average returns as well as rejects the null-hypothesis of zero intercepts, that with a single factor the specification of factor exposures is not enough to assimilate all of the return predictive content in stock characteristics. However, when considering a risk structure with two or more dimensions, the improvement in model fit due to non-zero intercepts becomes small and statistically insignificant. This suggests that risk exposures are well described by characteristics, and that the residual return predicability from characteristics makes "anomaly" intercepts unnecessary.
The IPCA also offers a test for which characteristics are significant for factor loadings and expected returns. With this, five characteristics are found to be significant at the 1% level. These include size, recent stock trends (such as momentum), and market beta, but does not include book-to-market equity or earnings-price measures.
The IPCA Model
The general IPCA model specification for an excess return is:
where ft+1 is a K-vector of latent factors, βi,t represents the dynamic factor loadings, zi,t is an instrument vector containing observable asset characteristics, and Γβ defines the mapping of characteristics and risk factor exposures. The IPCA model can be considered as an extension to the statistical approach of previous PCA models that allows for the consideration of pre-specified factors.
Asset Pricing Tests
The authors also introduce a set of statistical asset pricing tests. The first is designed to test the zero alpha condition that distinguishes the restricted and un- restricted IPCA models. The second tests whether observable factors significantly improve the model’s description of the panel of asset returns while controlling for IPCA factors. The third tests the incremental significance of an individual characteristic or set of characteristics while simultaneously controlling for all other characteristics.
Asset Pricing Tests
The authors also introduce a set of statistical asset pricing tests. The first is designed to test the zero alpha condition that distinguishes the restricted and un- restricted IPCA models. The second tests whether observable factors significantly improve the model’s description of the panel of asset returns while controlling for IPCA factors. The third tests the incremental significance of an individual characteristic or set of characteristics while simultaneously controlling for all other characteristics.
Test 1: Testing the zero alpha condition
The authors define the null hypothesis H0 as alphas are unassociated with characteristics.
Formally stated,
and
If we reject H0 in favor of H1, we can further determine which characteristics are most responsible for the rejection.
Test 2: Testing observable factor models versus IPCA
The IPCA model is extended to include common models with pre-specified observable factors. The result is:
where gt+1 is a vector of observable factors. Loadings on observable factors are allowed to be dynamic functions of the same conditioning information entering into the loadings on latent IPCA factors:
The encompassing model imposes the zero alpha restriction so that competing models can be evaluated on their ability to price assets based on exposures to systemic risk.
Test 3: Testing Instrument Significance
To test incremental significance of an individual characteristic is to check whether the characteristic impacts any of the pre-specified K factor loadings. Formally,
This is to say the lth row of the gamma vector must be zero.
Conclusion
IPCA represents a low-dimension factor model that can successfully describe riskiness of stocks as well as risk compensation while significantly outperforming existing factor models. The asset pricing tests introduced offer a new research protocol for further work in empirical asset pricing.

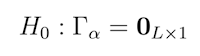

No comments:
Post a Comment