Campbell R. Harvey and Yan Liu. “Lucky Factors” Working Paper
This paper proposes a new testing method to select amongst a large group of candidate factors. The proposed method is based on a bootstrap approach that allows for general distributional characteristics of both factor and asset returns, for the possibility of time-series and cross-sectional dependence, and accommodates a wide range of test statistics. The proposed method allows us to mitigate the common, prevailing problem in empirical asset pricing studies - the test multiplicity and related data-snooping problem. Also, the method can be applied to both portfolio sorts as well as individual stocks. The proposed method is useful for answering questions such as determining which fund manager has outperformed or selecting which number and/or type of factors to include in an asset pricing model to better explain the cross-section of asset returns. More generally, the suggested method can be applied to specify a regression model when a researcher is faced with multiple variables to choose from and seeks to improve the explanatory power of the model as best as he or she can.
Following the organization of the paper, I first present in this summary how we can implement the proposed method in the context of predictive regression models and briefly for panel regression models. After that, an example of the application of the method in selecting amongst candidate (or suggested) factors based on the "incremental contribution" of a factor from the given candidate list.
Predictive Regression Models
Suppose we have a T x 1 vector Y of returns we want to predict and a T x M matrix X that includes the time-series of M right-hand side variables. The goal is to select a subset of the M regressors to form the best predictive regression model. An arbitrary performance measure for "goodness of fit" is denoted as Ψ. The bootstrap-based selection method is done in three steps.
[Step 1: Orthogonalization Under the Null]
Assume k variables are already selected and we want to test if there exists another significant predictor among the M-k candidate variables. The null hypothesis is that none of these candidate variables provide additional explanatory power of Y.
The goal of this orthogonalization step is to modify the data matrix X such that the null hypothesis appears to be true in-sample. To do so, one should first predict Y onto the group of pre-selected k variables and obtain the projection residual vector. Then, one should orthogonalize the M-k candidate variables so that no candidate variable is correlated with that projection residual vector. This procedure can be expressed as below;
Obtain projection residuals for candidate factors
with the regression below
Again, this procedure ensures that M-k orthogonalized candidate variables are uncorrelated with projection residual vector with respect to Y in-sample.
[Step 2: Bootstrap]
This second step involves bootstrapping time periods (rows in this example) to generate the empirical distributions of the summary statistics for different regression models. The suggested rule is that when there is little time dependence in the data, simply treat each time period as the sampling unit and sample with replacement. When time dependence is an issue, use a block bootstrap. As only time periods are resampled, it is possible to keep the cross-section information intact in the data structure, allowing us to preserve the contemporaneous dependence among the variables. One example transformation of the original data for this step is presented in the figure below;
With the bootstrapped sample, one runs M-k regressions. The associated summary statistics coming out from those regressions can be shown as below;
This statistic measures the performance of the best fitting model that augments the pre-selected regression model with one variable from the list of orthogonalized candidate variables. Max statistic is adopted to control for multiple hypothesis testing.
In this sense, the above-explained bootstrap approach allows one to obtain the empirical distribution of the max statistic under the joint null hypothesis that none of the M-k variables is true. The empirical distribution can be expressed as below;
where B denotes the number of bootstrap sampling iterations. This gives the distribution for the maximal additional contribution when the null hypothesis is true; i.e., the null of no predictability of the M-k variables is true. With this distribution with respect to null is given, we can move on to hypothesis testing.
[Step 3: Hypothesis Testing and Variable Selection]
If the decision is positive, declare the variable with the largest test statistic from the original data matrix X as significant and include it in the selected list in addition to the previous k selected factors. Then, repeat step 1 to step 3 to test for the next predictors.
Panel Regression Models
Overall bootstrap apporach is similar for panal regression models expect that the orthogonalization process is done by demeaning factor returns such that the demeaned factors have zero impact in explaining the cross-section of expected returns. This can also be better illustrated with the example below;
Baseline model with only one pre-selected factor (f1t)
Augmented model with an additional factor, f2t
If f2t is helpful in explaining the cross-section of expected returns, the intercept from the second regression model should be closer to zero than that from the first. The objective of orthogonalizing here is to adjust f2t such that the adjusted f2t guarantees the intercepts from those two regressions are nearly the same, which is to create a pseudo factor related to the null hypothesis of no incremental explanatory power. The detailed process for doing so is described below;
We can clearly see that the two alphas are equalized during this orthogonalization process. Following bootstrapping and hypothesis testing procedures are analogous to what has been explained above for predictive regression models.
Application: Selecting among 14 Candidate Factors
The suggested bootstrap method for panel regression model is applied to 14 risk factors that are proposed by existing asset pricing literature. The 14 potential risk factors are;
- profitability (rmw)
- investment (cma)
- market (mkt)
- size (smb)
- book-to-market (hml)
- profitability (roe)
- investment (ia)
- betting againist beta (bab)
- gross profitability (gp)
- Pastor and Stambaugh liquidity (psl)
- momentum (mom)
- quality minus junk (qmj)
- co-skewness (skew)
- common idiosyncratic volatility (civ)
These 14 factors are treated as candidate risk factors, and a researcher adopting the proposed method incrementally selects the group of factors.
The test statistics are scaled intercepts, which are expressed as below;
The results are presented in the following tables;
We can see that, after the inclusion of market, size, and book-to-market factors, in sequence, no other factors contribute to additional explanatory power in the model. The authors also emphasize that the market factor single-handedly reduces the average pricing error by 20%, much larger than the reduction in pricing error by alternative factors. Overall, the presented results indicate that, in contrast to recent asset pricing research, the original market factor is the most important factor in explaining the cross-section of expected returns.




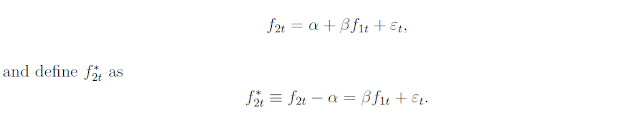


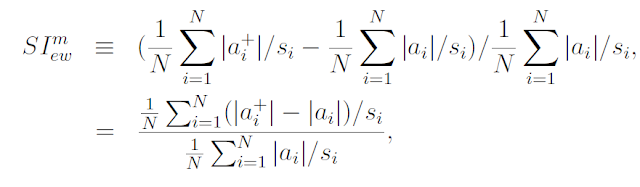


No comments:
Post a Comment